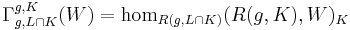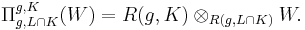Zuckerman functor
This article is about the Zuckerman induction functor, which is not the same as the (Zuckerman) translation functor.
In mathematics, a Zuckerman functor is used to construct representations of real reductive Lie groups from representations of Levi subgroups. They were introduced by Gregg Zuckerman (1978). The Bernstein functor is closely related.
Contents |
Notation and terminology
- G is a connected reductive real affine algebraic group (for simplicity; the theory works for more general groups), and g is the Lie algebra of G. K is a maximal compact subgroup of G.
- L is a Levi subgroup of G, the centralizer of a compact connected abelian subgroup, and *l is the Lie algebra of L.
- A representation of K is called K-finite if every vector is contained in a finite dimensional representation of K. Denote by WK the subspace of K-finite vectors of a representation W of K.
- A (g,K)-module is a vector space with compatible actions of g and K, on which the action of K is K-finite.
- R(g,K) is the Hecke algebra of G of all distributions on G with support in K that are left and right K finite. This is a ring which does not have an identity but has an approximate identity, and the approximately unital R(g,K)- modules are the same as (g,K) modules.
Definition
The Zuckerman functor Γ is defined by
and the Bernstein functor Π is defined by
Applications
References
- David A. Vogan, Representations of real reductive Lie groups, ISBN 3764330376
- A. Knapp, David A. Vogan, Cohomological induction and unitary representations, ISBN 0691037566 prefacereview by D. BarbaschMR1330919
- David A. Vogan Unitary Representations of Reductive Lie Groups. (AM-118) (Annals of Mathematics Studies) ISBN 0691084823
- G. J. Zuckerman, Construction of representations via derived functors, unpublished lecture series at the I. A. S., 1978.